Calculates the process capability indices Cp, Cpk, Cpl, Cpu, Cpm, Cpmk for a qcs object and normal distribution. Also, this function calculates confidence limits for \(C_p\) using the method described by Chou et al. (1990). Approximate confidence limits for \(C_{pl}\), \(C_{pu}\) and \(C_{pk}\) are computed using the method in Bissell (1990). Confidence limits for \(C_{pm}\) are based on the method of Boyles (1991); this method is approximate and it assumes the target is midway between the specification limits. Moreover, calculates the process capability indices CNp, CNpk, CNpm, CNpmk for a qcs object. A histogram with a density curve is displayed along with the specification limits, a Quantile-Quantile Plot for the specified distribution and contour graph is plotted for estimate the index Cpm.
Usage
qcs.ca(
object,
limits = c(lsl = -3, usl = 3),
target = NULL,
std.dev = NULL,
nsigmas = 3,
confidence = 0.9973,
plot = TRUE,
main = NULL,
...
)Arguments
- object
qcs object of type
"qcs.xbar"or"qcs.one".- limits
A vector specifying the lower and upper specification limits.
- target
A value specifying the target of the process. If it is
NULL, the target is set at the middle value between specification limits.- std.dev
A value specifying the within-group standard deviation.
- nsigmas
A numeric value specifying the number of sigmas to use.
- confidence
A numeric value between 0 and 1 specifying the probabilities for computing the quantiles. This values is used only when
objectvalues is provided. By defaultconfidence=0.9973.- plot
Logical value indicating whether graph should be plotted.
- main
Title of the plot.
- ...
Arguments to be passed to or from methods.
References
Montgomery, D.C. (1991) Introduction to Statistical Quality Control, 2nd
ed, New York, John Wiley & Sons.
Tong, L.I. and Chen, J.P. (1998), Lower con???dence limits of process capability
indices for nonnormal process distributions. International Journal of Quality & Reliability Management,
Vol. 15 No. 8/9, pp. 907-19.
Vannman, K (1995) A Unified Approach to Capability Indices. Statitica Sinica,5,805-820.
Vannman, K. (2001). A Graphical Method to Control Process Capability. Frontiers in Statistical Quality Control,
No 6, Editors: H-J Lenz and P-TH Wilrich. Physica-Verlag, Heidelberg, 290-311.
Hubele and Vannman (2004). The E???ect of Pooled and Un-pooled Variance Estimators on Cpm When Using Subsamples.
Journal Quality Technology, 36, 207-222.
Examples
library(qcr)
data(pistonrings)
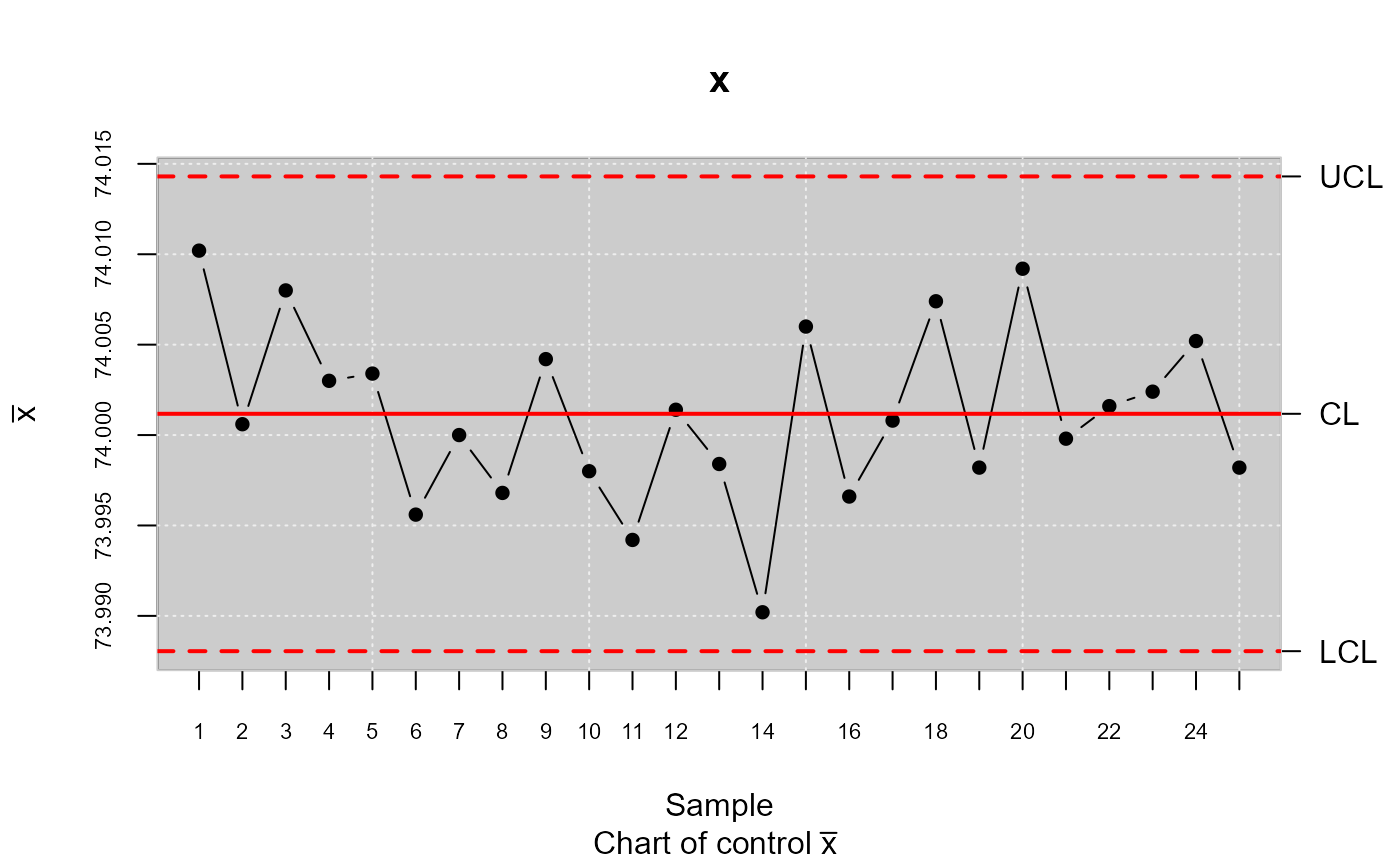
xbar <- qcs.xbar(pistonrings[1:125,],plot = TRUE)
 LSL=73.99; USL=74.01
limits = c(lsl = 73.99, usl = 74.01)
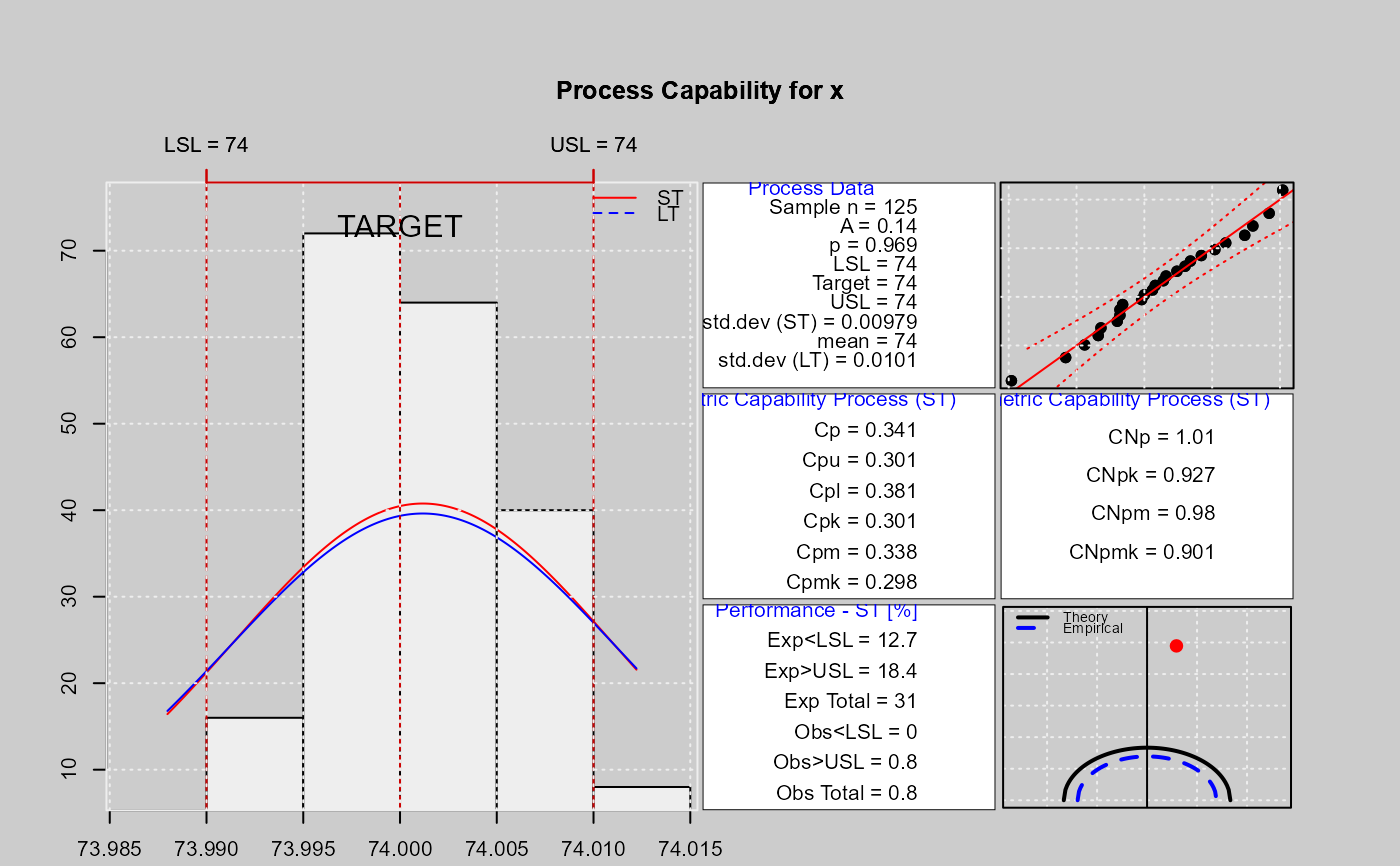
qcs.ca(xbar, limits = limits)
#>
#> Process Capability Analysis
#>
#> Call:
#> qcs.ca(object = xbar, limits = limits)
#>
#> Number of obs = 125 Target = 74
#> Center = 74 LSL = 73.99
#> StdDev = 0.009785 USL = 74.01
#>
#> Paremetric Capability indices:
#>
#> Value 0.1% 99.9%
#> Cp 0.3407 0.2771 0.4065
#> Cp_l 0.3807 0.2739 0.4875
#> Cp_u 0.3006 0.2021 0.3991
#> Cp_k 0.3006 0.1944 0.4068
#> Cpm 0.3382 0.2749 0.4038
#>
#>
#> Non parametric Capability indices:
#>
#> Value
#> CNp 1.0082
#> CNpK 0.9275
#> CNpm 0.9799
#> CNpmk 0.9015
#>
#>
#> PPM:
#>
#> Exp<LSL 1.267e+07 Obs<LSL 0
#> Exp>USL 1.836e+07 Obs>USL 8e+05
#> Exp Total 3.103e+07 Obs Total 8e+05
#>
#> Test:
#>
#>
#> Anderson Darling Test for normal distribution
#>
#> data: xbar
#> Error in round(x$statistic, 4): non-numeric argument to mathematical function
LSL=73.99; USL=74.01
limits = c(lsl = 73.99, usl = 74.01)
qcs.ca(xbar, limits = limits)
#>
#> Process Capability Analysis
#>
#> Call:
#> qcs.ca(object = xbar, limits = limits)
#>
#> Number of obs = 125 Target = 74
#> Center = 74 LSL = 73.99
#> StdDev = 0.009785 USL = 74.01
#>
#> Paremetric Capability indices:
#>
#> Value 0.1% 99.9%
#> Cp 0.3407 0.2771 0.4065
#> Cp_l 0.3807 0.2739 0.4875
#> Cp_u 0.3006 0.2021 0.3991
#> Cp_k 0.3006 0.1944 0.4068
#> Cpm 0.3382 0.2749 0.4038
#>
#>
#> Non parametric Capability indices:
#>
#> Value
#> CNp 1.0082
#> CNpK 0.9275
#> CNpm 0.9799
#> CNpmk 0.9015
#>
#>
#> PPM:
#>
#> Exp<LSL 1.267e+07 Obs<LSL 0
#> Exp>USL 1.836e+07 Obs>USL 8e+05
#> Exp Total 3.103e+07 Obs Total 8e+05
#>
#> Test:
#>
#>
#> Anderson Darling Test for normal distribution
#>
#> data: xbar
#> Error in round(x$statistic, 4): non-numeric argument to mathematical function