Capability Analysis

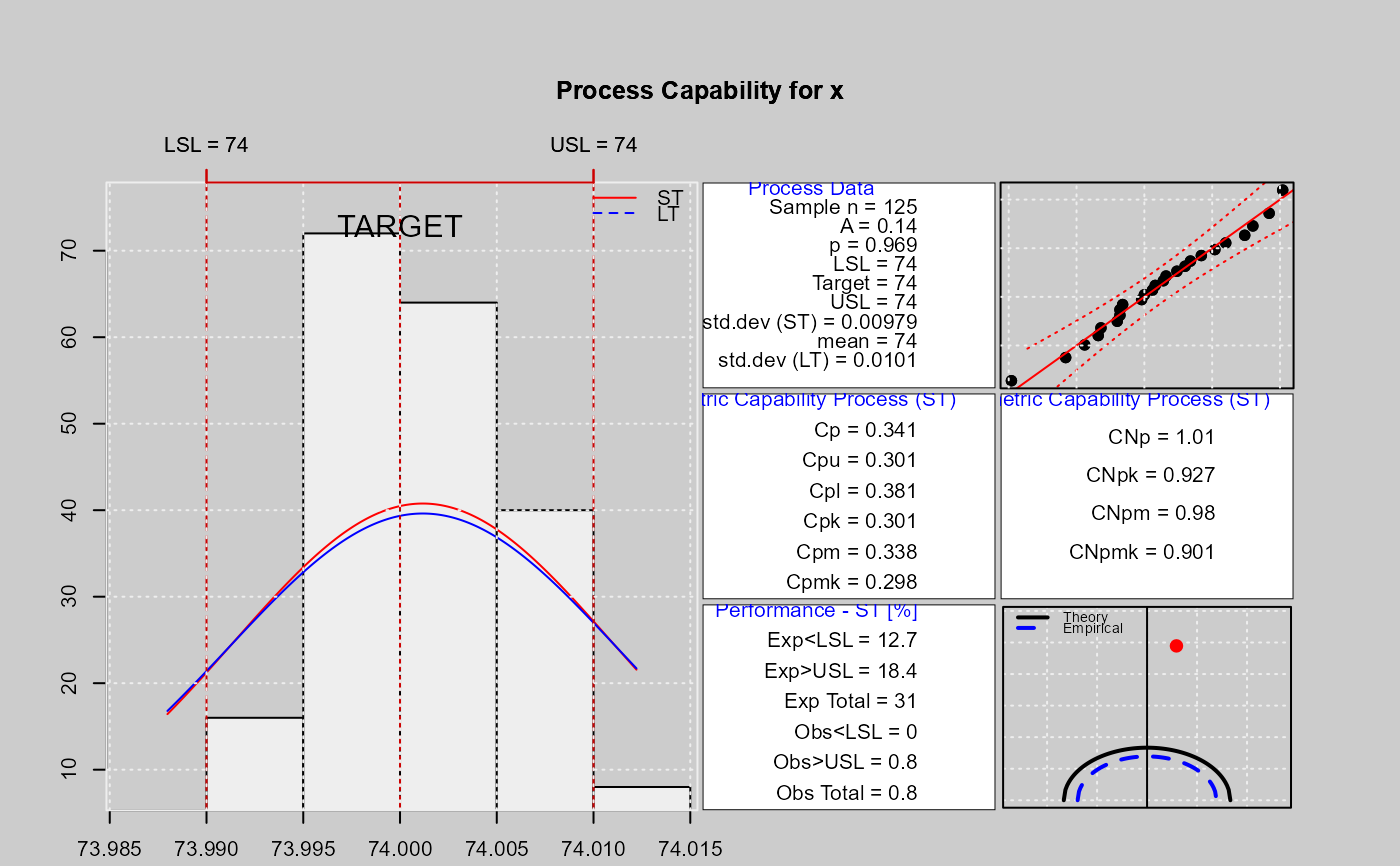
Calculates the process capability indices Cp, Cpk, Cpl, Cpu, Cpm, Cpmk for a qcs object and normal distribution. Also, this function calculates confidence limits for \(C_p\) using the method described by Chou et al. (1990). Approximate confidence limits for \(C_{pl}\), \(C_{pu}\) and \(C_{pk}\) are computed using the method in Bissell (1990). Confidence limits for \(C_{pm}\) are based on the method of Boyles (1991); this method is approximate and it assumes the target is midway between the specification limits. Moreover, calculates the process capability indices CNp, CNpk, CNpm, CNpmk for a qcs object. A histogram with a density curve is displayed along with the specification limits, a Quantile-Quantile Plot for the specified distribution and contour graph is plotted for estimate the index Cpm.

Usage

qcs.ca(
  object,
  limits = c(lsl = -3, usl = 3),
  target = NULL,
  std.dev = NULL,
  nsigmas = 3,
  confidence = 0.9973,
  plot = TRUE,
  main = NULL,
  ...
)

Arguments

object

qcs object of type "qcs.xbar" or "qcs.one".

limits

A vector specifying the lower and upper specification limits.

target

A value specifying the target of the process. If it is NULL, the target is set at the middle value between specification limits.

std.dev

A value specifying the within-group standard deviation.

nsigmas

A numeric value specifying the number of sigmas to use.

confidence

A numeric value between 0 and 1 specifying the probabilities for computing the quantiles. This values is used only when object values is provided. By default confidence=0.9973.

plot

Logical value indicating whether graph should be plotted.

main

Title of the plot.

...

Arguments to be passed to or from methods.

References

Montgomery, D.C. (1991) Introduction to Statistical Quality Control, 2nd ed, New York, John Wiley & Sons.
Tong, L.I. and Chen, J.P. (1998), Lower con???dence limits of process capability indices for nonnormal process distributions. International Journal of Quality & Reliability Management, Vol. 15 No. 8/9, pp. 907-19.
Vannman, K (1995) A Unified Approach to Capability Indices. Statitica Sinica,5,805-820.
Vannman, K. (2001). A Graphical Method to Control Process Capability. Frontiers in Statistical Quality Control, No 6, Editors: H-J Lenz and P-TH Wilrich. Physica-Verlag, Heidelberg, 290-311.
Hubele and Vannman (2004). The E???ect of Pooled and Un-pooled Variance Estimators on Cpm When Using Subsamples. Journal Quality Technology, 36, 207-222.

Examples

library(qcr)
data(pistonrings) 
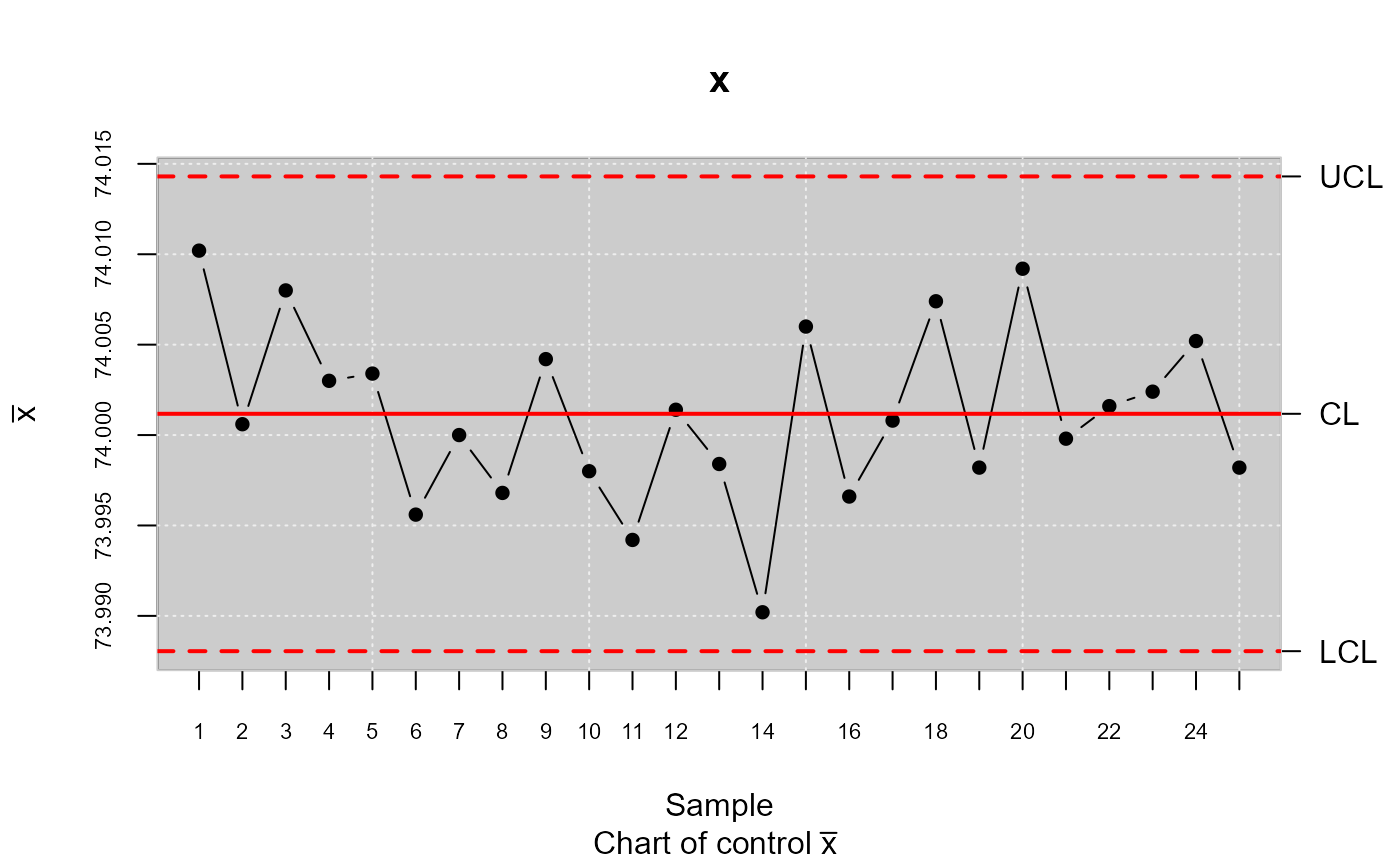
xbar <- qcs.xbar(pistonrings[1:125,],plot = TRUE)

LSL=73.99; USL=74.01
limits = c(lsl = 73.99, usl = 74.01)
qcs.ca(xbar, limits = limits)
#> 
#> Process Capability Analysis
#> 
#> Call:
#> qcs.ca(object = xbar, limits = limits)
#> 
#> Number of obs = 125          Target = 74
#>        Center =  74               LSL =  73.99
#>        StdDev =  0.009785         USL =  74.01
#> 
#> Paremetric Capability indices:
#> 
#>        Value    0.1%   99.9%
#> Cp    0.3407  0.2771  0.4065
#> Cp_l  0.3807  0.2739  0.4875
#> Cp_u  0.3006  0.2021  0.3991
#> Cp_k  0.3006  0.1944  0.4068
#> Cpm   0.3382  0.2749  0.4038
#> 
#> 
#> Non parametric Capability indices:
#> 
#>         Value
#> CNp    1.0082
#> CNpK   0.9275
#> CNpm   0.9799
#> CNpmk  0.9015
#> 
#> 
#> PPM:
#> 
#>          Exp<LSL 1.267e+07       Obs<LSL 0
#>          Exp>USL 1.836e+07       Obs>USL 8e+05
#>        Exp Total 3.103e+07     Obs Total 8e+05
#> 
#> Test:
#> 
#> 
#> 	Anderson Darling Test for normal distribution
#> 
#> data:  xbar 
#> Error in round(x$statistic, 4): non-numeric argument to mathematical function