Skip to contents

Process capability indices (Nonparametric)

Source: R/qcs.cpn.r
qcs.cpn.Rd

Calculates \(CNp\), \(CNpm\) using the formulation described by Tong and Chen (1998).

Usage

qcs.cpn(
  object,
  parameters = c(u = 0, v = 0),
  limits = c(lsl = -3, usl = 3),
  q = c(lq = -3, uq = 3),
  target = NULL,
  median = 0,
  nsigmas = 3,
  confidence = 0.9973
)

Arguments

object

qcs object of type "qcs.xbar" or "qcs.one".

parameters

A vector specifying the u and v parameters values. If parameters = c(u=0, v=0), the CNp indice is calculed; If parameters = c(u=1, v=0), the CNpk indice is calculed; If parameters = c(u=0, v=1), the CNpm indice is calculed; If parameters = c(u=1, v=1), the CNpmk indice is calculed.

limits

A vector specifying the lower and upper specification limits.

q

A vector specifying the lower and upper quantiles. These values are necessary, if object value is missing.

target

A value specifying the target of the process. If it is NULL, the target is set at the middle value between specification limits.

median

A value specifying the median of data.

nsigmas

A numeric value specifying the number of sigmas to use.

confidence

A numeric value between 0 and 1 specifying the probabilities for computing the quantiles. This values is used only when object values is provided. By default confidence=0.9973.

References

Montgomery, D.C. (1991) Introduction to Statistical Quality Control, 2nd ed, New York, John Wiley & Sons.
Tong, L.I. and Chen, J.P. (1998), Lower confidence limits of process capability indices for nonnormal process distributions. International Journal of Quality & Reliability Management, Vol. 15 No. 8/9, pp. 907-19.

Examples

library(qcr)
##' data(pistonrings) 
xbar <- qcs.xbar(pistonrings[1:125,],plot = TRUE)

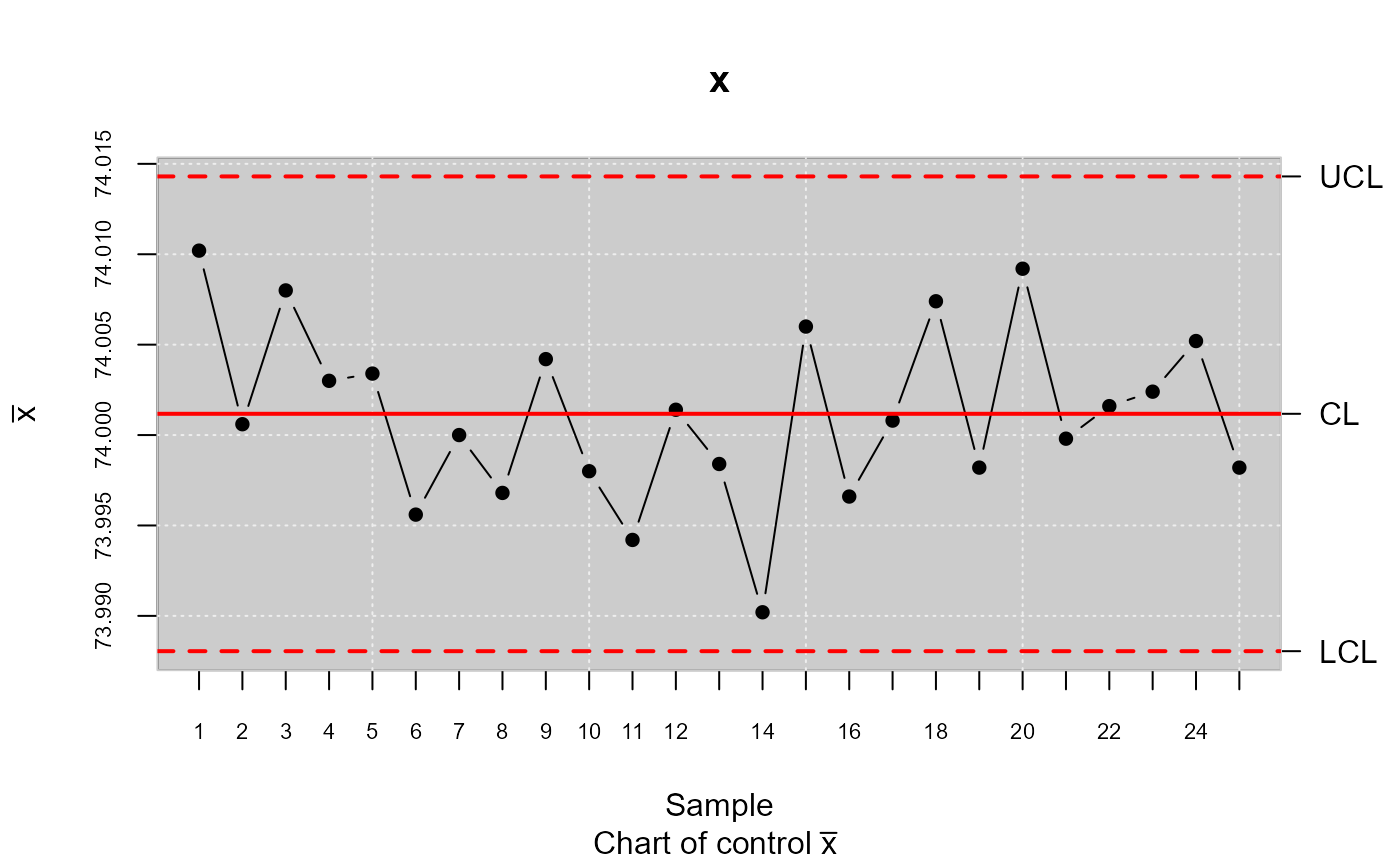x<-xbar$statistics[[1]]
LSL=73.99; USL=74.01
median <-median(x)
lq=as.numeric(quantile(x,probs=0.00135))
uq=as.numeric(quantile(x,probs=0.99865))
qcs.cpn(parameters = c(0,0),limits = c(LSL,USL),
       median = median, q=c(lq,uq))
#>    CNp 
#> 1.0082 
qcs.cpn(object = xbar,parameters = c(0,0), limits = c(LSL,USL))
#>    CNp 
#> 1.0082 
qcs.cpn(object = xbar,parameters = c(1,0), limits = c(LSL,USL))
#>   CNpk 
#> 0.9275 
qcs.cpn(object = xbar,parameters = c(0,1), limits = c(LSL,USL))
#>   CNpm 
#> 0.9799 
qcs.cpn(object = xbar,parameters = c(1,1), limits = c(LSL,USL))
#>  CNpmk 
#> 0.9015